Entanglement is perhaps the purest form of the strangeness of quantum mechanics. Bell’s Theorem is perhaps the purest demonstration of this, producing a result that is squarely at odds with classical notions of reality. Below is the simplest description of quantum entanglement and Bell’s theorem that I’ve come across, and I haven’t seen it descried in blog form anywhere, so I thought I’d share. And it doesn’t require any physics knowledge at all. As Feynman may have said, “If you think you understand quantum mechanics, you don’t understand quantum mechanics.” This is my best attempt at explaining why.¹

The Experiment

Three people, creatively named 1, 2 and 3, are a few light-minutes from each other and from a central source.

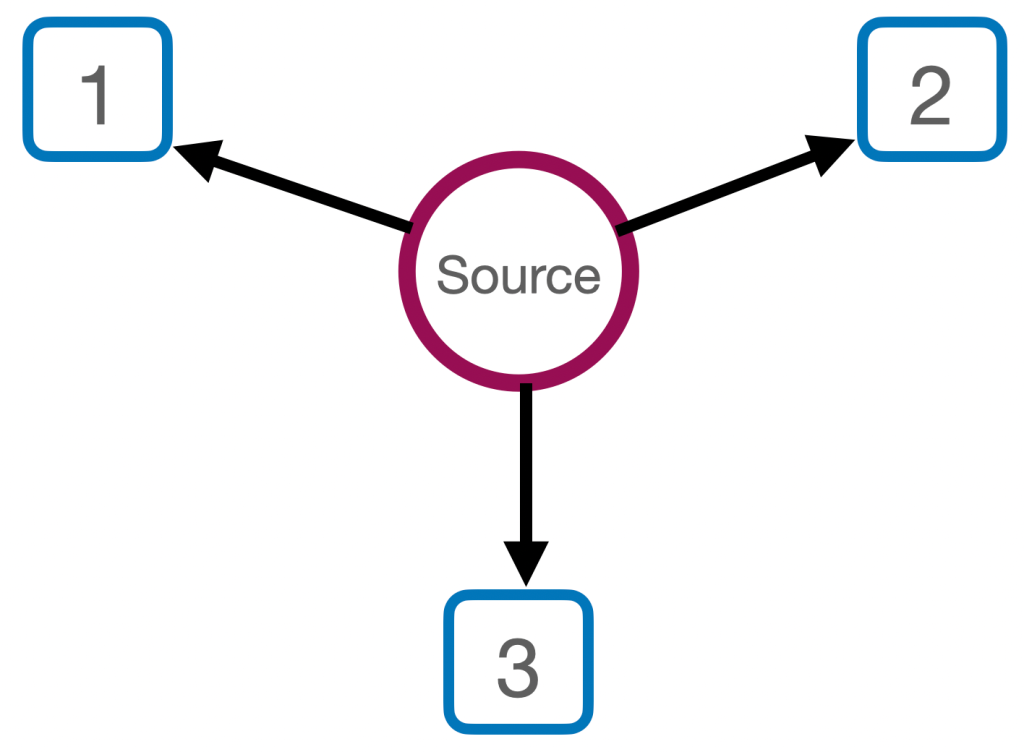
Each person has a measuring device. It has a knob that they can switch between A and B, and a pair of lights, labeled + and -. Once a minute, something from the source is sent to all three people. Of course, it takes several minutes to get to them. Before it gets there, each person independently sets their knob to either A or B at random. When the thing arrives, the device measures it and one of the two lights turns on. The person then records both the knob position (A or B) and which light lit up (+ or -).

How do they set it “at random”? They could just guess a random A or B each time². Or they could flip a coin, and if it lands heads they pick A. Or they could use a random number generator in a computer. Or they could use a little circuit that switches between A and B once every nanosecond, and stops when they press a button. Nobody can time their presses to within a nanosecond, so the result is effectively random. Or you could use everybody’s favorite random process, and get a radioactive sample that has a 50% chance of decay in, say, every 10 second period. Then choose a 10 second period, and if it decays in that time, set it to A, if not, B. Our crowd source their choices, by having a website where people can vote A vs B and take the one that gets the most votes. Or use a telescope to observe a distant star that flickers randomly, whose light left the star millions or billions of years ago.

And so, once a minute, they make an entry in their log, until they have thousands of entries. Then they bring the entries together to compare them, looking something like this:

Time	Person 1	Person 2	Person 3
12:00	A+	B-	B-
12:01	A+	A-	B-
12:02	B+	B+	A+
12:03	A-	B+	B-
…	…	…	…

Then they analyze the results. Each person notices, when the knob is set to A, they get a plus 50% of the time, and therefore minus the other 50%. Same when set to B. And when you compare any two people’s results, say person 1 and person 3, no matter what their knob settings, you all readings equally. That is, whether the two knobs were set to AA, AB, BA or BB, you get ++, +-, -+ and — each 25% of the time.

So far, this isn’t very interesting. The device could be ignoring whatever came from the source, ignoring the knob and just returning some arbitrary result. You don’t need quantum mechanics to explain that. However, when one observer chooses A, and the other two choose B, you notice a pattern: there are either one or three plusses. There are never two pluses, and never all three minuses. So the only observations we see, when one knob is A and the other two are B, are:

And each are equally likely, happening 25% of the time. So when 1 observes A+, and 2 observes B+, then we know that if 3 is set to B the result will be +. Even if 3 is set to A, we know that if it had been set to B, we would have gotten +.

In fact, if person 1 measures A and gets +, then we know that 2 and 3’s B measurements would be the same, either both + or both -. Similarly, if person 2 measures A and gets +, then we also know that 1 and 3’s B measurements would be the same. So, in minutes when persons 1 and 2 both measure A and get +, we know that 2’s B must be the same as 3’s B, which must be the same as 1’s B. So we can conclude that all 3 B’s must be the same, which mean’s 3’s A measurement must be +. Just look at the right hand table above.

So we have a prediction: in the minutes when all three knobs were set to A, and the first two both measured +, then the third one must measure +! So we race to the data and what do we see? The exact opposite! Whenever the first two are A+, A+, and the last one is A, it’s always A-! Every. Single. Time.³

So what’s going on under the hood?

If you think about it, this is quite strange. Are all thee Bs the same when we don’t measure them? If so, then how could the third A be -? If not, then how does person 3’s device know what’s going on with 1 and 2’s devices?

There are a couple possibilities:

1. Local Realism: The three particles decide, before they leave the source, which light they’ll trigger for both A and B. For example, perhaps the particle going to 1 is in a state where, when the knob is A it gives +, and for B gives -. We can write that as A+B-. Same for the other two. The problem is, our observations above have ruled that out.
2. Superdeterminism: Maybe the source somehow knew how the knobs would be set, even though they weren’t set until several minutes after the particles left. Perhaps the source knew some previous state of the three people and their devices, and could 100% accurately simulate everything, including the psychology of a person who chooses A vs B, the biology and physics of a coin flip, the psychology of the crowd during the crowd sourcing, and the light that left the star millions of years ago and hasn’t reached the source yet. Or perhaps the source is deterministic too, and the entire universe has been scripted down to the tiniest detail, including what the knobs will be set to and where the particles will end up. And it’s not just deterministic, but coordinated, so that the particle that leaves the source is somehow in just the right state for whatever the switch will be set to. Seems unlikely.
3. Spooky action at a distance: Perhaps, when the first person makes a measurement, some influence travels instantly to the other two particles, changing their state. One problem with this is, thanks to Einstein’s special theory of relativity, some other observer would see the influence happen backwards in time. In other words, the properties of the other two would be set before the measurement, in some reference frames.
4. It Simply Is: Quantum Mechanics rejects all three of the above. The particles aren’t in any definite state, of either A or B, until they are measured. The act of measurement, including which property A or B is being measured, affects the system as a whole.

So faster than light communication then?

Unfortunately no. We can’t use this to communicate information. If person 1 measures along A and gets +, that means 2 and 3 will get the same along B. If person 1 gets -, they’ll get the opposite. But even if 2 and 3 move their devices next to each other and compare notes in real time, they can’t tell what setting person 1’s knob was set to. In fact, even whether or not person 1 makes a measurement can’t be determined by just looking at person 2 or 3. And this isn’t just in our experiment, it’s a general theorem of quantum mechanics, called the No-communication theorem.

Digging Deeper

The strangeness of quantum mechanics comes from combining three things:

1. That states can be modeled with probability amplitudes, complex numbers. When a particle can be in multiple states at once, called superposition, we add the probability amplitudes, resulting in interference. The Born rule states that the probability of observing the particle in a given state is the square of the magnitude of the probability amplitude. A great demonstration of this is the double slit experiment with electrons.
2. Complementarity, which includes and Heisenberg’s Uncertainty principal. Mathematically, that some pairs of observables fail to commute.
3. Entanglement. Superposition where each state in the superposition is a multi-dimensional state, so that the state of one dimension depends on the state of another dimension.

Footnotes

1. It’s a slight simplification of Sidney Coleman’s description in Quantum Mechanics In Your Face (and the transcript). I’m very grateful to Mark Weitzman for pointing me to it, and in general for all his help in answering questions during my journey so far in quantum mechanics. ↩︎
2. People are actually bad at producing random sequences this way. For example, people tend to alternate choices more often than the 50% of time you’d get if each were truly random. But for our purposes we don’t need it to be completely random. If you don’t like the idea of each person trying to choose randomly, just ignore that and focus on one of the other methods. ↩︎
3. For those who do know quantum mechanics, the source is sending three spin one-half particles in the state and A and B correspond to and . ↩︎