Update: This kinda blew up! Featured in Hacker News, Ars Technica and PC Gamer, among others.
Just months after Neil Armstrong’s historic moonwalk, Jim Storer, a Lexington High School student in Massachusetts, wrote the first Lunar Landing game. By 1973, it had become “by far and away the single most popular computer game.” A simple text game, you pilot a moon lander, aiming for a gentle touch down on the moon. All motion is vertical and you decide every 10 simulated seconds how much fuel to burn.
I recently explored the optimal fuel burn schedule to land as gently as possible and with maximum remaining fuel. Surprisingly, the theoretical best strategy didn’t work. The game falsely thinks the lander doesn’t touch down on the surface when in fact it does. Digging in, I was amazed by the sophisticated physics and numerical computing in the game. Eventually I found a bug: a missing “divide by two” that had seemingly gone unnoticed for nearly 55 years.
Landing with Maximum Fuel
To use the least fuel while landing, you need to land in the shortest time possible. Initially you maximize your speed by keeping your engine off, then at the last possible second you burn full throttle, reducing your speed to zero just as you touch the surface. The Kerbal Space Program community calls this a “suicide burn”, since getting the timing right is hard and it leaves no room for error.
With some trial and error and a bit of (manual) binary search, you can find the schedule that just barely has you landing. You burn nothing for 70 seconds, then 164.31426784 lbs/sec for the next 10 seconds, then the max 200 lbs/sec after that:
The game considers a perfect landing to be less than 1 MPH, but here we land at over 3.5 MPH and are told we “could be better.” Yet burn even 0.00000001 more lbs/sec, and you miss the surface entirely, ascending at 114 MPH:
How did we go from a hard landing to not landing at all, without a soft landing in between?
Physics Simulation: One Smart Kid
I expected to see the simple Euler integration that’s common in video games even today. That’s where you compute the forces at the start of each time step, then use F=ma to compute the acceleration, then assume the acceleration is constant over a time step of 
Because the mass is changing over the timestep, the acceleration will change too, so assuming it’s constant is only approximate. But surprisingly, Jim used the exact solution, the Tsiolkovsky rocket equation, with a Taylor series expansion for the logarithm. He also used some algebra to simplify it and reduce the amount of round off error. Very impressive for a high school senior in 1969. When I asked him about it:
“I was skilled at calculus at the time and familiar with concepts like a Taylor series, but also my recollection is that my father, who was a physicist, helped me in the derivation of the equations.” – Jim Storer, personal communication
The rocket equation is what gives rise to the suicide burn being optimal, and the five terms he uses of the Taylor series, where the argument is at most 0.1212, makes it accurate to over six decimal places. So that’s not the problem we’re looking for.
Assumptions Go Out The Window When We Hit The Ground
The rocket equation works well until you hit the ground. In general, collisions between solid objects is a really hard part of dynamics engines, and what separates the great ones from the good ones, as I discovered when contributing to Open Dynamics Engine as a postdoc at MIT.
And this is where the Lunar Landing Game faces its biggest challenge. Imagine the lander descending at the start of a 10-second turn but ascending by the end. Simply verifying that it’s above the surface at both points isn’t enough. It might have dipped below the surface somewhere in between. When this happens, the program has to rewind and examine an earlier moment.
An obvious place is to look at the lowest point of the trajectory, where the velocity is zero. For the rocket equation, it turns out, there’s no closed form expression for that lowest point that involves only basic mathematical functions.1 So instead, we can use the physicists favourite technique, and take only the first few terms of the Taylor series. If you use only the first two terms of the logarithm, the problem simplifies to a quadratic equation and you can use the good old quadratic formula from high school. And the approximation should be pretty good over the space of a 10 second turn, accurate to within 0.1% or so.
But that’s not what Jim did. His formula has a square root in the denominator, not the numerator. It also had an error 30 times bigger.
How To Know When You’ve Hit Rock Bottom
What could he possibly be doing? I stared at this for a long time, wracking my brain for any other approach to approximate the bottom of the trajectory that would still only use addition, subtraction, multiplication, division and square root. Taking only the first term of the logarithm would give an approximation worse than the quadratic, but wouldn’t involve a square root. Taking a third term and we need to solve a cubic, which in general would need a lot more code and in our case it doesn’t seem to be of any special form that has a simple solution2. There are many approximations to 
Until I looked a little more closely at his square root. It’s of the form:
Which looks a awful lot like the quadratic formula where we’ve divided by 4 inside the square root. It has to be related. But why is it in the denominator? Did he find a quadratic in 
And this alternate form has a key advantage. Because once we discover that we’ve hit the ground, we need to go back and find the time where we hit the ground. And we do the same thing, truncating the Taylor series to give us a quadratic. And in that case, the original form has a divide by zero when the leading coefficient is zero. That happens when the thrust from the rocket engine exactly balances the force of gravity. And that’s probably common for many players, who hover over the surface and gently descend. And they don’t need to be exactly equal. If the thrust is close to the force of gravity, you can get catastrophic cancellation in the numerator, then the tiny denominator blows up your errors. This alternate form is much more numerically stable, and in fact works just fine when the quadratic term is zero, so we actually have a linear equation and not quadratic. It’s amazing to me that Jim would either somehow re-derive it, or learn it somewhere. I don’t think it’s taught in textbooks outside numerical computing, and I don’t think it’s even common in physics.
Let’s Double Check The Derivation
But if his formula is equivalent, then why is the approximation error 30 times higher? Deriving the formula ourselves, we get:
Which is identical to Jim’s code, except … he’s missing the 2 in the denominator inside the square root! It was probably a simple error, either when deriving the formula or typing it into the computer. After all, the computer algebra system MACSYMA had only started a year before, and wouldn’t be available at a high school, so he would have had to do everything using pencil and paper.
With this bug, he consistently underestimates the time to the lowest point. He compensates for this two ways: adding 0.05 sec, and then re-estimating from his new, closer location. And this explains why it misses the time of landing: the first estimate is while the lander is above the surface and still descending, then the second one is after reaching the bottom and ascending again, which takes less than 0.05 sec.
If we add the missing factor of two and remove the 0.05, what happens? Now the best we can do with a suicide burn is:
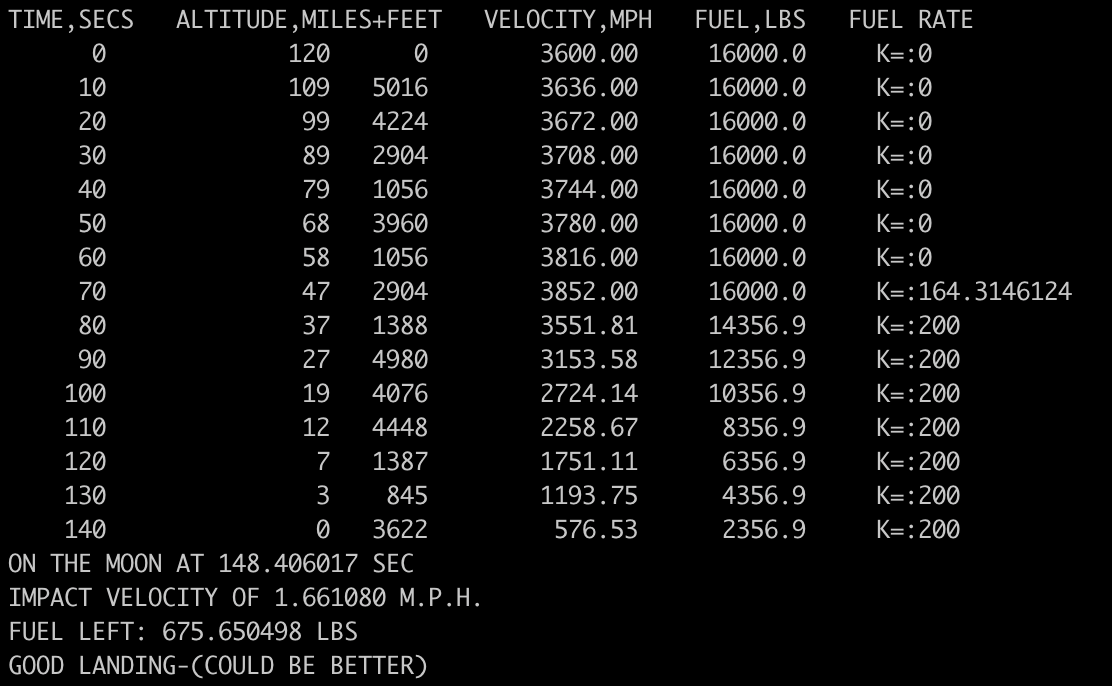
Our velocity is down to 1.66 MPH, almost three quarters of the way to the perfect landing at 1 MPH. It’s not perfect because we’re still only using the first two terms of the Taylor series. Also, once you’ve decided your lowest point is under the surface, you then need to find the time where you first hit the surface, which involves a similar approximation. Another iteration would help, although with the bug fixed we overestimate the time, so we’d need to go back in time, which might mean we have to pick the other solution to the quadratic. You could simplify that by using only a single term from the Taylor series, and is what’s done in Newton’s method. You could then stop when the magnitude of the velocity is below some threshold, and use the altitude there to decide whether or not you landed. But this is all more work, and the game was fun to play as it is, so why complicate the code?
It’s also possible to land gently, you just need to end your 14th turn with a low altitude and velocity, and then use low thrust in your 15th turn, landing somewhere after 150 seconds. It’s just the theoretical full-thrust-on-landing suicide burn, that takes around 148 seconds, that eludes us.
CAPCOM We’re Go For Powered Descent
Overall, this is very impressive work for an 18 year hold high school student in 1969 on a PDP-8. This was long before Computer Science was taught in high school. The numerical computing aspects, such as iteratively improving the estimate using Newton’s method or worrying about catastrophic cancellation, weren’t well known back then. I didn’t learn them until I was studying for a Ph.D. in robotics.
It is also surprising that, as far as I can tell, this bug has been there for almost 55 years and nobody has noticed it before. That’s probably because, even with the bug, it was a fun game, both difficult and possible to land gently. The quest to not just win, but find the optimal strategy, can certainly lead to trying to understand small discrepancies. I suspect everybody else was just happy to play the game and have fun.
- It needs the Lambert W, the inverse of
↩︎
- For example,
, where the 2nd and 3rd coefficients have the same magnitude but different sign, can be factored in the form
, which has solution
↩︎
Martin C. Martin 
In 1983 I found a bug in the Lunar Lander version for the TRS-80: https://archive.org/details/80-microcomputing-magazine-1983-12/page/n269/mode/1up?q=seth
This game launched my CS career. It was available in my Webster, NY High school running on a Xerox owned Data General Eclipse. I was later able to use Xerox Star network on weekends. Got to Cornell and was appalled at their mainframe punch card classes. Learned genetics instead. I later was at U of AZ using C programming in astronomy informatics. Then NM Tech VLA and LANL on the US Human Genome Project. That early exposure is what we promote at the Supercomputer Challenge. https://supercomputingchallenge.org/ My son was writing Kerbal python code and now builds Medical AI.
Looks like the bug exists also in Dave Ahl’s 101 BASIC Computer Games
A few years ago I found another bug in a Pascal transcoding of the game:
mistakenly recognizing the Taylor series of the logarithm of (1-x) with -ln(1+x).
https://retrocomputing.stackexchange.com/q/15820/4025
Cool. The Taylor series for -ln(1+x) would have alternating signs: -x + x^2/2 – x^3/3 + …
For + ln(1+x), they also alternate but obviously opposite of above: +x – x^2 + x^3/3 + …
So yes, if the signs were alternating, they’re mistakenly using ln(1+x). If the signs are all the same, it’s + or – ln(1-x) though.
The reconstituted Pascal code has the equivalent of
x := deltaT * value / mass;
newVmps := Vmps + lunarG * deltaT – LN(1.0 + x) * impulse;
(pardon the extra parentheses),
where in BASIC the signs were all the same:
Q = S*K/M
J = V+G*S+Z*(-Q-Q*Q/2-Q^3/3-Q^4/4-Q^5/5)
Is corrected code posted anywhere?
The following git repo has the C code fix for the lunar lander code
https://github.com/ericeche/lunarlanderc
I loved reading about your deep dive into figuring this out. Any interest to being a guest on the Legacy Code Rocks[1] podcast to chat about it more with me?
[1]: https://legacycode.rocks
I would love to! I can think of some other things to talk about: I got interested because I found my old cassette tapes with my Apple ][ & Vic-20 programs on them, had fun figuring out which was which, got a game King working, then decided to find the optimum strategy for it. In doing so, I found a bug in it, and contacted the author, one Jim Storer, who pointed me to his Lunar Lander page.
Anyway, we could have a fun discussion of old computer tech, how you store a computer program as audio, the book BASIC Computer Games, which was the first computer book to sell over one million copies, “kids, when we were young and wanted to play a game, we had to type in the listing, and a single typo meant it might not work.” When I first got my VIC-20, which cost more than a MacBook Air does today, I didn’t have a cassette drive. I typed in a program, and that night my parents saw I’d left the computer on and turned it off, erasing all my hard work!
Also, Jeff Atwood of Stack Overflow and Coding Horror fame, has started a community project to port all these old games to modern scripting languages. So that meshes well with “modernizing software applications.”
I filled out the “suggest a guest” form on your website with my email, so get in touch at your convenience.
Small typo, missing the “e” in “we’re”
The legacy code written in C adds 0.5 sec instead 0.05 sec as described in the article :
https://www.cs.brandeis.edu/~storer/LunarLander/LunarLanderTranslations/LunarLanderJohnsonTranslation-c.txt
Original 112 line from C code
S = M * V / (Z * K * (W + sqrt(W * W + V / Z))) + 0.5;
After correcting line 112:
S = M * V / (Z * K * (W + sqrt(W * W + V / (2 * Z)))) ;
and running the simulation, the simulation lands with sucess:
COMMENCE LANDING PROCEDURE
TIME,SECS ALTITUDE,MILES+FEET VELOCITY,MPH FUEL,LBS FUEL RATE
0 120 0 3600.00 16000.0 K=:0
10 109 5016 3636.00 16000.0 K=:0
20 99 4224 3672.00 16000.0 K=:0
30 89 2904 3708.00 16000.0 K=:0
40 79 1056 3744.00 16000.0 K=:0
50 68 3960 3780.00 16000.0 K=:0
60 58 1056 3816.00 16000.0 K=:0
70 47 2904 3852.00 16000.0 K=:164.3146124
80 37 1388 3551.81 14356.9 K=:200
90 27 4980 3153.58 12356.9 K=:200
100 19 4076 2724.14 10356.9 K=:200
110 12 4448 2258.67 8356.9 K=:200
120 7 1387 1751.11 6356.9 K=:200
130 3 845 1193.75 4356.9 K=:200
140 0 3622 576.53 2356.9 K=:200
ON THE MOON AT 148.41 SECS
IMPACT VELOCITY OF 1.66 M.P.H.
FUEL LEFT: 675.65 LBS
GOOD LANDING-(COULD BE BETTER)
I just fixed a 32-year old bug in another game (funnily, also involving a lunar lander), but you have surely trounced me with this one.
https://github.com/raceintospace/raceintospace/issues/847
Nice article!
Small typo: in footnote two, the leading term should be a cube, not a square.
Thanks! You should write a blog post about how you found a bug, in my blog post about finding a bug in Lunar Lander. 🙂
I tried a version for comparison just leaving out the additional 0.05 (omitting the bug repair) and it worked for the suicide burn, basically by doing another loop of 3.10, which activates 8.10 for a second time (not needed after bugrepair). 1.67 MPH can be achieved.
After signalling (in the same way), things work out identically, and the extreme sensitivity is gone; 1.67 MPH results from the same tweaked value as in the article.
Part of the explanation is that 8.10 only signals (and sometimes runs away when doing a suicide burn at the last possible moment when it (incorrectly or not) thinks ground level is not reached on the lowest point), but the real work of determining landing conditions is done in 7.10, which repeats the work on the last turn by iteratively computing constant mass landing time, computing the full results (9.10, apply_thrust() in the C translation) until landing is established (S<0.005).
It would change the character of the game, but one could devise conditions in the final landing where human intelligence can be assumed to switch the engine off and achieve a landing instead of allowing a fly-off. That is, assuming that the engines can be switched off on a short enough notice. If the 10 seconds interval for commands is realistic, i.e. the engine(s) are slow to respond, everything stays the same.
The end of the signalling loop (8.10) is weird. It checks J and V separately, after calling update_lander_state(), which sets V to J. The J check was perhaps intended before update_lander_state(), but updating is necessary.
Also the translation to C is not exact at that point. Focal has `I (-J)3.1,3.1`, meaning execute 3.1 when -J is smaller or equal to 0.
The equal part was left out in C, or perhaps the -J < 0 was intended as J > 0.
I am also just guessing at the reasons why this check (in addition to the V check) is needed. It sort of echos the opening condition that J and V are opposite in direction, but I do not understand yet.
Ah, a kindred spirit. A suicide burn should land with as close to zero velocity as possible. When you mention that 8.10 runs away, do you mean as your touch down velocity gets closer to zero? That’s what I would expect. Since 8.10 (with the bug) always undershoots, and the code waits until it overshoots, it should get into an infinite loop, although if you get lucky with round off errors it might exit at the end.
And yes, absolutely about 7.10. As you say, it computes an estimate of the landing time based on constant mass, which will be an underestimate if you’re burning fuel at all. But then it iterates until it gets a time step of 0.005, “close enough.”
But actually, when burning the full 200 lbs/sec, 0.005 might still be too far. Velocity changes by about 600 MPH in the turn before, so a rough estimate is that, in 0.005 sec, velocity could change by
MPH, so not quite precise enough to get within 1 MPH. What happens if you change that threshold to 0.001 or smaller? Can you achieve a suicide burn with velocity < 1 MPH? That would be a cool addendum to the post.
I’m not sure what you mean by that. That’s what currently happens, as soon as you make contact with the ground, the game assumes you shut the engine off. Or do you mean at the bottom of the trajectory where velocity is zero, even if you’re still above the ground?
I agree that the code that checks both J and V, when they’re the same, doesn’t seem to do what the author thinks. As written, it always branches to 3.1 and never to 8.1. As you say, they probably meant to be comparing the old velocity with the new.
Please let me know if you have any new insights, and thanks again for your critical eye.
Thanks for a great reply.
Devise … I meant, as you suggested, not flying off when the lowest point is at positive altitude, especially like less than 10 meters or so, or what ever would agree with a goal. For example, the goal can accept a “could be better” or even “poor” landing without damage.
Switching off engine at lowest point above moon then would be quite preferential at less than 20 ft or 100 ft altitude depending on which is the 2 goals is chosen as acceptable.
And one could go further, assuming switching off at lowest point is pretty much an instinctive reaction.
Lastly and obviously, the code required can easily be done in Focal, so is not an anachronism for reasons of programming language or length of program.
Further insight (hopefully):
The increase of .05 seconds to TF in the original code (8.10, testing for contact, negative/zero altitude) may be interpreted as allowing for an engine switch off before end of turn close to the surface, such as discussed as an addition to the program (see devise).
.05 seconds is just a trifle more than allowable for a 1 mi/s impact (perfect) landing. So if this triggers negative altitude, land. It is then conceivable to put this in again together with the bugfix (in the C translation, it was accidentally replaced with 0.5 as noticed before)
The condition at the end of 8.10 is meant to repeat 8.10 (or not) as indicated in 8.30 (then looking again for a contact without reading a new input) which only makes sense when V>0 and TF (T) is greater than zero (or 0.001). The T(F) check is necessary before repeating 8.10 (otherwise 3.1 for new input).
I am tempted then to replace the -J test by the T test. Pity that the timeleft test has to be coded twice, but otherwise an unwanted apply_thrust() occurs instead of a further ground contact test.
Impact: The ground contact routine 8.10 is not applied that often. Usually negative altitude will be found at the end of a turn, then going to loop_until_on_the_moon without using 8.10. So this all may be a bit marginal to begin with.
https://github.com/janhec/moonlander
Quite experimental.
Thanks for the code! One thing I noticed, if you put the bug back in so it underestimates the time to zero velocity, but make that 0.05 constant much lower, e.g. 0.0005, then I got it to land with a velocity of 0.007886 M.P.H., using fuel @ t = 70 of 164.314709089. In the code that actually finds the zero altitude, I changed that constant to 0.0001.
Might have taken unreasonably long on a PDP-8 to do that many iterations. Also, I think the accuracy of the floating point was only between 5 and 6 decimal digits, whereas with double precision on modern hardware you get something like 14 to 15. But with those changes I do get a very gentle “perfect” landing in 148.429019 sec.
Trying to use your inputs on original and modified version of Jim Storer’s code in FOCAL on emulated TSS8 (simh pdp8). The results are actually not that different with an impact velocity of 5 M.P.H.
So original version was probably good enough considering available FOCAL implementation at that time.
Great Article! I just wanted to mention that the alternative form of the quadratic formula just comes from taking the usual formula and using the technique of “multiplying by the conjugate”. This is a very common and useful technique for manipulating algebraic equations. It can be used whenever you want to rationalize a numerator or denominator with two terms.