Mother’s parser doesn’t follow the convention. It’s not generated from a specification by ANTLR, yacc or another parser generator. It’s a program, just like any other. It’s currently written in Java. Perhaps some day it will be rewritten in Mother itself.

[Talk about how it’s extensible. About hacking on Cython, and the experimentation that was possible because of its simple recursive-descent parser. Define “user code” as code that extends the parser, that’s in a library, not in Mother’s core.]

[Maybe have a “pros & cons” section on not using a parser generator. Cons: don’t get tool support (although I think I could get some tools support if I had ASTNode extend ANTLR’s equivalent). Not as concise (although maybe a DSL would help). Pros: Could create a parser DSL, which would have all the power of Mother, like rake vs. make. More flexible: your grammar doesn’t have to fit into LL(1) or whatever. For example, optional newlines in Groovy require a special token, “nls!”, to match the newlines, and this has to be put everywhere a non-significant newline could appear. It shows up ??? times in the grammar. Something that common is easy to leave out in one or two places. In Mother’s parser, we can put it right in the nextToken() and peek() functions, and for the most part, the grammar doesn’t have to worry about it.]

It’s a top down operator precedence parser, but don’t worry if obscure computer science articles from the 1970s scare you. It’s actually very simple.

[Describe the basics]

An Example

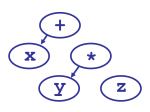
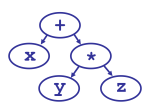
The tricky part of parsing is knowing what to group with what. For example, we know that * is more important than +, so that x + y * z means “first compute y * z, then add that to x.” In the jargon, we say that * has higher precedence than +.

So how does parsing work? Well, first we split the input into tokens,

[Pseudo code for expression() function, identifier’s NUD, and + and *’s LED. Point out that each call to expression() starts by grabbing something with a null denotation (i.e. a terminal or a prefix operator), and after that only grabs things with left denotations (anything that comes after its first subexpression, e.g. infix and postfix operators.]

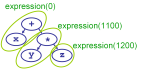
Recursion is often kind of confusing. Let’s trace through an example. Let’s see how it parses x + y * z.

We start by calling expression(right_binding_power=0). What it does is:

• Takes the next token (in this case, the first token, x) and calls its null denotation, which just returns the token itself.

• Then we compare our right_binding_power to the left_binding_power of the next token, +. Its binding power is higher, so we take this token and call its left denotation, passing it the x. It will use the x for its left child.

• To get the right child, +‘s left denotation calls expression() recursively, this time with a right_binding_power of 1100.
• This second call to expression() grabs the next token, y, and calls its null denotation, which just returns y itself.
• It then compares its right_binding_power, 1100, to the left_binding_power of the next symbol, *, namely 1200. Since 1100 < 1200, the second call grabs the * and calls its left denotation, passing it y.

• *‘s left denotation calls expression(right_binding_power=1200).
• This third call to expression() takes the next token, z, and calls its null denotation, which just returns the token itself.
• It then looks at the next token, EOF, and compares the right_binding_power, 1200, to EOF’s left_binding_power of zero. Since 1200 is not less than 0, the third call just returns the z.

• *‘s left denotation now makes a tree out of the y that was passed in, and the z that was returned from the third call to expression.

• It returns the tree to its caller, expression(1100), which compares its right_binding_power, 1100, to the next token’s, EOF’s, left_binding_power of 0, and returns.
• Finally, +’s left denotation makes a tree out of the x that was passed in, and the y * z that was returned by expression(), and returns it.

• Back in the first call to expression(0), we compare our right_binding_power, 0, to the next token’s, EOF’s, left_binding_power of 0, and return the tree.

So, to summarize, the first call to expression() handles the x and +, the second call (initiated by +‘s left denotation) handles the y and *, and the third one handles the z.

What happens when * comes before +? The first call to expression() grabs the x, then handles both the + and the *. The second call (called by *‘s left denotation) handles the y, and the third one (called by +‘s left denotation) handles the z.

Tips on Extending The Parser

When parsing a construct, ask yourself:

• What’s the first token where you can identify the construct? For example, if you were introducing a >.. range operator, then when parsing (x * y) >.. z, the first place where you can tell it’s a range is when you see the >...

• Anything before that will be parsed without knowing that it’s part of your construct. But once we’re in the code for >.., you can modify the parse tree arbitrarily.

• In that first token’s MOS or SOS, you only know what’s come before that token. So, if the parse tree depends on what comes later in the string, you can either look at the next few tokens to try to disambiguate things, or return some data structure representing the “parts,” and let some later token’s MOS decide how it should be parsed.

• [You can add something to the ParseContext, once we have a ParseContext.]

For example, consider the parsing of types, such as the return type of a method, or the type of a local variable. It would be great if we could just recognize a type from looking at its tokens, without having to know whether we’re in a local variable definition or the argument list of a method definition. But when we see:

final Foo …

we can’t tell whether Foo is the name of a variable or a type, since it could continue either:

final Foo = 23

or

final Foo foo = 23

This could be resolved a couple different ways:

• Add a bit to the ParseContext to tell whether a name is required. However, there may be cases where the context isn’t sufficient. It also limits the ability of people to extend the parser, since the tokens to the left of the type must unambiguously tell whether or not a name is expected, and the name can’t be optional.

• Pick an arbitrary choice, and leave it to the caller or later tokens to change it if it turns out to be wrong. In the above example, we could always parse Foo as a type, and let the parser for the variable definition change it to the variable name if no name follows.

• Have a rule like “if its followed by an identifier, it must be a type, but if it’s followed by an =, ; or new line, its not.” However, this means you couldn’t extend the parser to include any construct with a type at the end of a statement.

On a completely different note: prefer a recursive formulation to an iterative one, because it allows others to extend your work. For example, the first version of the parser for class parsed the declaration in the SOS of modifier or, if there was no modifier, the class token. But one of the primary ways of extending Mother is adding a new keyword to replace class, e.g. immutableclass, or to add delegates where you have extends and inherits. With all of this parsed “top down” in a single function, it’s impossible to extend it without copying the function and modifying it; and then you can’t have two people modifying it.

So, the “bottom up” method, of letting every token define it’s own parsing behavior, is much more flexible.

Adjacency and Optional Parentheses

One curious fact about our parser as described above is that it always expects an operator to separate two subexpressions. So it needs to be able to handle Mother’s optional parentheses, where the function and its first argument appear one after the other, for example, myfunction argument.

One difference between this type of parser and those generated from a BNF-like grammar, is that in Mother’s parser the code executed for each rule must be attached to a token, as either itsstartOfSubexpression or middleOfSubexpression function. This is a problem for parsing method calls with optional parentheses: the source code “f x” has only two tokens, with no operator connecting them.

And we still need to process precedence as above, so we can parse x + f y (where the function is “f” and the argument “y”) as well as x . f y (where the function is “x . f” and the argument is still y). So in places where a subexpression is followed by another subexpression, with no operator in between, the Mother parser inserts a virtual token, with type "(adjacent)".

How does it know where one subexpression ends and another begins, while it’s still in the middle of parsing? On the one hand, we’d like the tokenizer to insert this virtual token, so the built-in expression() function and all user code see exactly the same sequence of tokens. On the other hand, we want user code to be able to parse token streams however it wants, ignoring the normal interpretation of those tokens if it likes.

The solution is to not have the tokenizer insert the “(adjacent)” token, but rather to have a simple rule for when they’re inserted, a rule that’s implemented by the expression() function, and is simple enough that user code can easily implement it. What’s the rule? Well, whenever you’re done parsing a subexpression, look at the next token. If it has no left denotation, then it can’t be an operator and better have LBP 0. And if it does have a null denotation, then it could start another subexpression, unlike closing tokens such as ) or separating tokens such as , or else. In this case we pretend the next token is actually “(adjacent)”.

Declarative vs. Bottom Up

If you look at the code, you’ll notice that certain symbols will match and consume other symbols in their SOS or MOS. For example, “(” will consume the matching “)”. This is a great way to implement things that must always go together, but you might be tempted to parse an entire, complex construct in a single SOS or MOS. Or at least I was, until I tried it.

It was my second attempt at parsing definitions. The things that declare local variables, fields, methods and classes. I wrote a single big function to do the whole thing. It would match all the modifiers (like public and synchronized), then the optional class name, []s for arrays, check to see if there was a “(” indicating a method, etc. The problem is, it wouldn’t have been extendable.

The declaration of types is complex enough that someone might want to extend it. ML lovers might want to add something like ML’s rich type system. And Java’s has even been extended, with generic and annotations in Java 5.0.

So when possible, you should really write any complex syntax in a “bottom up” way of defining SOS and MOS for most of the tokens, and keeping those functions simple. Avoid the “top down” of doing it with loops all in one function.

By the way, the first attempt at parsing definitions was to do it using the existing expression() function and the expression SOSes and MOSes. But I ended up realizing it would be cleaner to give types a separate function (“definition()“) and their own set of SOSes and MOSes, because there was too much overlap with existing syntax. For example, in Java it’s perfectly legal (though discouraged) to define an array of strings like this:

String blah[] = new String[] {"foo"};

It’s too confusing, in the expression parser for “[“, to remember that “x[]” is actually valid, because it might not be an expression at all, it might actually be a declaration. I’m not planning to support that syntax in Mother, since it’s bad style in Java and, more importantly, nobody uses it. But still, I don’t want to bake a restriction like that into the very parser framework — maybe some ML guys will need it to do something that’s actually helpful.

Expression Closers

[Talk about C++’s problem with templates and >>. Talk about Mother’s general mechanism: normally any string of non-alpha numerics would be a single operator, but any startOfSubexpression/middleOfSubexpression can register a closer. It’s hidden by the next opener, so there’s only at most 1 closer being scanned for at any one moment.]

[Point to Crockford’s page for more info.]